


Überlegungen zur Abschätzung der Fluggeschwindigkeit, Flugweite und Flugzeit eines Golfballs nach dem
Treffmoment mit einem Driver (genauer Driverkopf).
[Hier als pdf version als auch in
Englischer Sprache]
Stefan Hippler, Heidelberg, 5. August 2006
Letzte Aktualisierung am 12. Februar 2024
Für ganz Eilige finden sich die Antworten zur Ballgeschwindigkeit in den Gleichungen 15 und 16. Für die Flugweite entsprechend in 18 und 20 und zur Flugdauer bitte ganz ans Ende gehen.
Die folgenden Überlegungen basieren auf den bekannten physikalischen Erhaltungssätzen von Energie \(E\) und Impuls \(p\).
Die Ausgangslage ist klar, der Golfball liegt ruhig auf dem Boden (Ballgeschwindigkeit \(v_B=0\)) und wird von einem
Golfschläger (Driver) getroffen, genauer gesagt von dessen Schlägerkopf. Sowohl Golfball als auch der Schlägerkopf
werden als vollkommen starr angenommen (elastischer Stoßvorgang). Die folgenden Formeln behandeln den
eindimensionalen Fall, der Schlägerkopf kommt horizontal von links und trifft den Golfball, der nach dem
Treffmoment horizontal nach rechts wegfliegt. So würde man beispielsweise den Zeitraum kurz vor und nach dem
Treffmoment sehen, wenn ein Golfspieler mit der rechten Hand den Golfball mit dem Driver vom Tee spielt und
der Beobachter, oder ein technisches Gerät wie eine Videokamera, den Spieler frontal betrachtet. Die
folgende Grafik visualisiert diese drei Phasen am Beispiel eines Golfschlags von Rory McIllroy (youtube).



Ganz kurz vor dem Treffmoment gilt für den Schlägerkopf: \begin {equation} \label {p1} p_0=m_S \cdot v_0 \end {equation} \begin {equation} \label {e1} E_0=\frac {1}{2}m_S \cdot v_0^2 \end {equation} Hierbei sind \(m_S\) die Masse des Golfschlägerkopfes und
\(v_0\) die Geschwindigkeit des Schlägerkopfes im Treffmoment. \(E_0\) ist die kinetische Energie des Schlägerkopfes und \(p_0\) sein
Impuls. Energie \(E_B\) und Impuls \(p_B\) des Golfballs sind vor dem Treffmoment 0.
Für den Gesamtimpuls \(p\) und die Gesamtenergie \(E\) von Golfball und Schlägerkopf vor dem Treffmoment gilt also: \begin {equation} \label {p1a} p = p_0 \end {equation}
\begin {equation} \label {e1a} E = E_0 \end {equation}
Ganz kurz nach dem Treffmoment gelten für Gesamtimpuls und Gesamtenergie: \begin {equation} \label {p2} p=m_S \cdot v_S + m_B \cdot v_B \end {equation} \begin {equation} \label {e2} E=\frac {1}{2}m_S \cdot v_S^2 + \frac {1}{2}m_B \cdot v_B^2 \end {equation} Hinzu gekommen ist der Impuls
des Golfballs der Masse \(m_B\) und Geschwindigkeit \(v_B\). Die gesamte kinetische Energie \(E\) ist nach dem Treffmoment
aufgeteilt in die kinetische Energie des Golfballs \(E_B = \frac {1}{2}m_Bv_B^2\) und des Schlägerkopfes \(E_S = \frac {1}{2}m_Sv_S^2\). Die Geschwindigkeit des
Schlägerkopfes \(v_S\) ist nach dem Treffmoment kleiner als vor dem Treffmoment, also \(v_S < v_0\). Gleiches gilt für die Energie
\(E_S < E_0\).
Jetzt lassen sich die Gleichungen 1, 3 und 5 zusammen fassen zu: \begin {equation} \label {r1} m_S \cdot v_0 = m_S \cdot v_S + m_B \cdot v_B \end {equation}
Das gleiche mit den Gleichungen 2, 4 und 6 ergibt: \begin {equation} \label {r2} \frac {1}{2}m_S \cdot v_0^2 = \frac {1}{2}m_S \cdot v_S^2 + \frac {1}{2}m_B \cdot v_B^2 \end {equation}
Weiter läßt sich Gleichung 8 geschickt umformen. Die Idee dazu findet sich beispielsweise im Buch Physics for Scientists and Engineers von Serway und Jewett auf den Seiten 235–237 der 7. Ausgabe von 2008. Dazu wird der Faktor \(1/2\) eliminiert und durch Umschreiben ergibt sich: \begin {equation} \label {r2b} m_S \cdot ( v_0^2 - v_S^2) = m_B \cdot v_B^2 \end {equation}
Die linke Seite kann faktorisiert werden. Hinweis: \((a^2-b^2) = (a-b)(a+b)\): \begin {equation} \label {r2c} m_S \cdot (v_0 - v_S) (v_0 + v_S) = m_B \cdot v_B^2 \end {equation}
Um die Idee der Vereinfachung zu erkennen, wird jetzt noch Gleichung 7 umgeschrieben zu: \begin {equation} \label {r1b} m_S \cdot (v_0 - v_S) = m_B \cdot v_B \end {equation}
Die Vereinfachung wird erreicht indem Gleichung 10 durch Gleichung 11 dividiert wird: \begin {equation} \label {EASY1} (v_0 + v_S) = v_B \end {equation} \begin {equation} \label {EASY2} v_0 = v_B - v_S \end {equation}
Diese Gleichung zusammen mit Gleichung 11 macht es sehr einfach, die Geschwindigkeiten von Golfball und Schlägerkopf kurz nach dem Treffmoment zu berechnen: \begin {equation} \label {HeadSpeedAfter} v_S = \frac {m_S - m_B}{m_S + m_B} \cdot v_0 \end {equation} \begin {equation} \label {MAXSPEED} v_B = \frac {2 m_S}{m_S + m_B} \cdot v_0 \end {equation}
Im Verlauf des Fluges wird die Geschwindigkeit des Balls \(v_B\) in der Regel natülich immer kleiner.
Jetzt können die Ergebnisse mit Zahlen aus der realen Welt überprüft werden. Der Golfball wiegt maximal \(m_B\) = 45,93 g. Ein Driver-Kopf hat eine Masse von ca. \(m_S\) = 200 g. Für die Schlägerkopfgeschwindigkeiten \(v_0\) kann eine sehr hohe von Bryson DeChambeau genommen werden, z.B. \(v_0\) = 240,4 km/h (149,4 mph). Mit Gleichung 15 kann die Geschwindigkeit des Golfballs kurz nach dem Treffmoment berechnet werden: \begin {equation} \label {MAXSPEED2} v_B = 391\,km/h = 243\,mph \end {equation}
Die berechnete Ballgeschwindigkeit ist in diesem Fall ca. 10% höher als die mit Trackman gemessene von
221,5 mph.
Da sich der Golfball bei einem Treffer mit dem Driverkopf verformt, außerdem das Schlägerblatt eines Drivers wie eine gespannte Membran arbeiten kann (Trampolineffekt) und auch noch andere Faktoren (Dimples, Spin) eine Rolle spielen, ist das ziemlich nahe dran an der maximalen Golfball-Geschwindigkeit, die real möglich ist. Ist die Golfballmasse vernachlässigbar gegen die Schlägerkopfmasse, ergibt sich die theoretisch maximale Geschwindigkeit des Golfballs zu: \begin {equation} v_B = 2 \cdot v_0 \end {equation}
Mit den angegebenen Zahlen ergibt sich eine Schlägerkopfgeschwindigkeit nach dem Treffmoment entsprechend Gleichung 14 zu \(v_S\) = 150,6 km/h (93,6 mph). Der Schlägerkopf wurde ordentlich abgebremst.
Für Freizeitgolfer mit Driverkopfgeschwindigkeiten vor dem Treffmoment von typischerweise unter 145 km/h
(90 mph), liegt die maximale Ballgeschwindigkeit entsprechend bei knapp 236 km/h (147 mph). Das liegt
nahe an den Geschwindigkeiten welche beim Aufschlag im Tennis von den besten Tennisspielern erzielt
werden.
Um die Flugweite des Golfballs abzuschätzen, ist neben der horizontalen auch die vertikale Richtung zu betrachten.
Damit wird die eindimensionale Betrachtungsweise wie für die Berechnung der Geschwindigkeiten verlassen und es ist
etwas mehr Mathematik nötig. Hilfreich ist ein Blick in den Wikipedia Artikel über die Wurfparabel. Dort wird die
maximale Reichweite vom Boden unter Vernachlässigung des Luftwiderstands mit: \begin {equation} \label {RMAX} R_{max} = \frac {v_B^2}{g} \cdot \sin {2\beta } \end {equation} angegeben. Hier bezeichnet \(g\)
die Erdbeschleunigung (9,81 m/s\(^2\)) und \(\beta \) den Wurfwinkel zur Horizontalen hin. Die Sinusfunktion wird maximal für \(\beta =45\)
Grad, also \(\sin {(2\cdot 45)}=1\).
Die Reichweite ist umgekehrt proportional zu \(g\), und somit beispielsweise auf dem Mond bei gleicher Geschwindigkeit \(v_B\)
etwa 6 mal so weit (\(g\)Erde=9.81m/s\(^2\), \(g\)Mond=1.66m/s\(^2\)).
Gleichung 18 gilt allerdings nur wenn der Luftwiderstand ignoriert wird. Wird er berücksichtigt, ergibt sich ein
optimaler Startwinkel \(\beta \) von ca. 20 Grad und die Parabelflugbahn knickt nach ihrem Maximum schnell
ab, das heißt, der Ball fällt fast senkrecht zu Boden. Die Reichweite wird auf ca. 64% (sin(2 * 20 Grad) =
0,64) der maximalen Flugweite reduziert.
Die Wikipedia Grafik zeigt dazu Flugtrajektorien für verschiedene Startwinkel.
Mit den bisher benutzten Werten, v\(_B\)=391 km/h und \(\beta \) = 20 Grad, ergibt sich somit eine maximale Ballflugweite nach Gleichung˜19 von
\begin {equation} \label {RMAX2} R_{max}(\beta =20\,Grad) = 772,9\,m. \end {equation}
Dies gilt wohlgemerkt nur für die angenommene Wurfparabel. Schaut man auf die im Profi-Golf mit dem Driver
erzielten Wurfwinkel (Launch Angle), liegen diese nach Trackman für die PGA Tour im Schnitt bei etwa bei 10
Grad.
Somit also 50% niedriger als der optimale Winkel einer Wurfparabel mit Luftwiderstand. Entsprechend ist die berechnete maximale Flugweite kürzer. Nehmen wir den gemessenen Wurfwinkel von 8,5 Grad aus den Daten von Bryson DeChambeau, sowie die vorher berechnete Ballgeschwindigkeit \(v_B\) = 391 km/h, ergibt sich die Flugweite zu:
\begin {equation} \label {RMAX3} R_{max}(\beta =8,5\,Grad) = 351,6\,m. \end {equation} Das stimmt überraschend gut mit der gemessenen Flugweite von 344,1 m überein.
Der wahre Ballflug ist deutlich komplexer, entsprechend sind auch die Flugweiten in der Realität anders und deutlich
geringer. Wer hier in die Tiefe gehen will, kann nach Publikationen mit den Schlüsselwörtern ”golf ball
aerodynamics” auf die Suche gehen. Einen Vorgeschmack auf die physikalische Beschreibung realistischer
Golfball-Flugtrajektorien bekommt man im frei zugänglichen eBook von Dr. Eugen Willerding im Kapitel
4.15.
Beispielhaft sind typische PGA Tour Trajektorien, wie sie von Trackman bestimmt wurden, in der folgenden Grafik
zu sehen (1 Yard \(\approx \) 0,9 m).
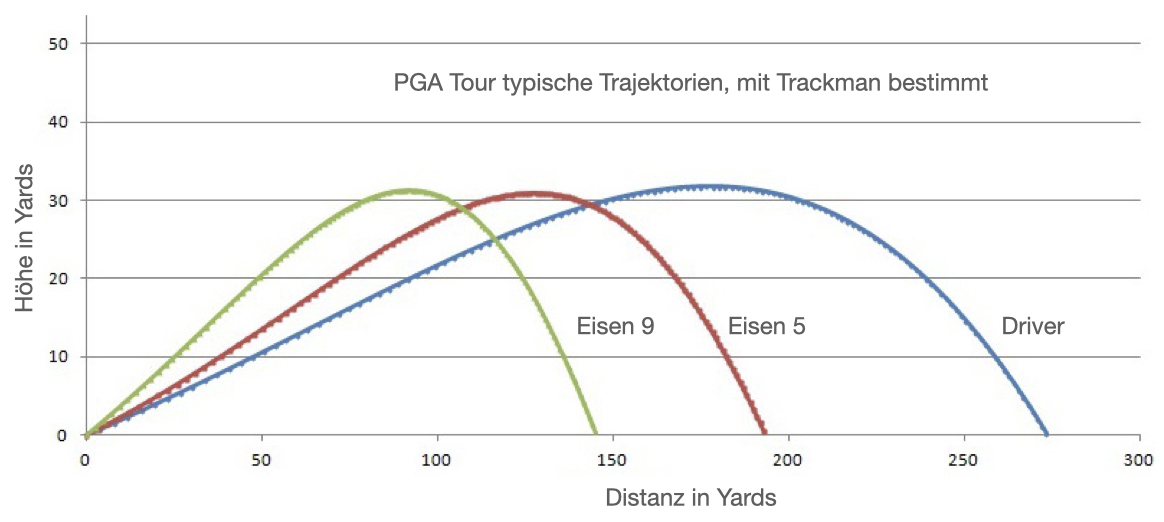
Hier geht es um die Frage wie lange der Golfball in der Luft fliegt, also vom Abschlag bis zur Landung auf dem
Boden. Im Englischen wird diese Zeit oft mit hang time bezeichnet. Schaut man sich die PGA Tour
Statistik dazu an, liegen diese Zeiten im Schnitt bei ca. 6,5 Sekunden, der Bereich in etwa zwischen 6 und 7
Sekunden.
Bitte nicht vergessen, diese Betrachtungen und Berechnungen beruhen auf vereinfachenden Annahmen.