Adaptive Optik Online mit Fokus auf die Astronomie AO Logo
Von Stefan Hippler und Andrei Tokovinin Heidelberg im Februar 2024
Korrektur optischer Turbulenz
Deformierbare Spiegel 		zum Inhaltsverzeichnis von
Adaptive Optik Online
Teilkorrigierte Bildaufnahmen
Wir nehmen an, dass alle atmosphärischen Aberrationen mit Skalen p und größer (also die niedrigen Moden bzw. niedrigen Raumfrequenzen) perfekt korrigiert werden. Wie sieht in diesem Fall die Strukturfunktion der verbleibenden, nicht korrigierten, Aberrationen aus? Rein qualitativ (siehe linkes Bild) nimmt die Strukturfunktion bis zum Abstand r=p zu und saturiert dann auf einem Niveau von zweimal der restlichen (unkorrigierten) Phasenvarianz σ2.

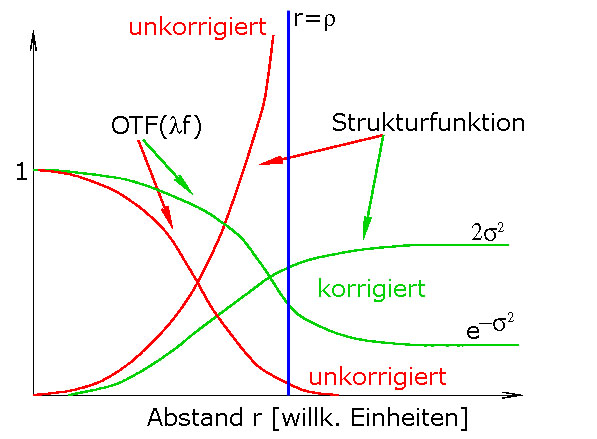
Die optische Übertragungsfunktion, OTF, ist proportional zu (siehe Gl. 6 im vorherigen Kapitel) \( \exp[-0.5D_\phi (\lambda \vec{f}) ] \). Sie fällt in diesem Fall nicht gegen 0 für große Raumfrequenzen f sondern wird konstant auf einem Niveau von
\[ S^* = e^{-\langle\sigma^2\rangle}. \hspace{1cm} (1) \]
Dabei wird S* wird als kohärente Energie bezeichnet.
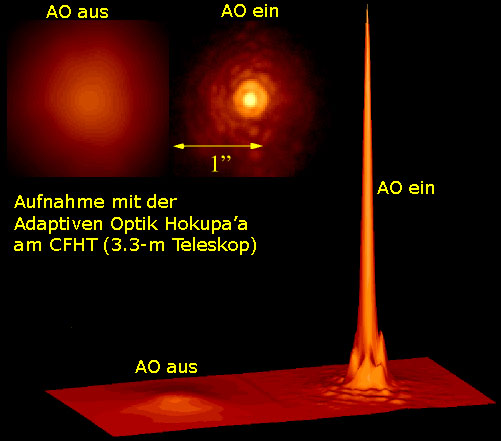
Für große Teleskope ist die Punktverteilungsfunktion, PSF, im Fall einer teilweisen Korrektur darstellbar als die Summe eines Seeing-limitierten Halos (1-S*)P' und eines beugungsbegrenzten Zentralbereichs S*P0: \[ P_{partial}(\vec{\alpha}) \approx (1 - S^*) P_a^{\prime}(\vec{\alpha}) + S^*P_0(\vec{\alpha}). \hspace{1cm} (2) \]
Das linke Bild zeigt eine typische teilkorrigierte Adaptive Optik PSF.

Für große Teleskope mit Spiegeldurchmesser D>>r0, im Beispiel ein 3.3-m Teleskop und ein r0 von 17cm im V-Band, ist das Halo sehr breit im Vergleich zum beugungsbegrenzten Zentralbereich. Die Aufnahmen wurden bei einer Wellenlänge von 0.936µm gemacht. Die Helligkeit des Referenzsterns (SAO 12442) für die Adaptive Optik ist V=9.5. Die am Referenzstern gemessene Halbwertsbreite betrug 0.6 Bogensekunden ohne Adaptive Optik (aus) und 0.068 Bogensekunden mit eingeschalteter Adaptiver Optik (ein). Die entsprechenden Strehlzahlen wurden mit 0.009 und 0.29 bestimmt. Die Integrationszeit betrug jeweils 30 Sekunden.

Mit eingeschalteter Adaptiver Optik dominiert die Zentralintensität die PSF und die Strehl-Zahl S ist in etwa gleich der kohärenten Energie S*. Diese Näherung wird oft benutzt, d.h. die Strehl-Zahl ist äquivalent zur kohärenten Energie, somit also S = S*. Diese Näherung für die Strehl-Zahl wird auch als Maréchal Näherung bezeichnet.
Frage: Welche Strehl-Zahl entspricht einer Phasenvarianz von 1 Quadratradian? Wie groß darf die Phasenvarianz maximal sein um eine Strehl-Zahl von 0.95 zu erreichen?

Frage: Die Strehl-Zahl sei bei einer bestimmten Wellenlänge, z.B. 0.5µm, bekannt. Wie berechnet sich daraus die Strehl-Zahl bei einer anderen Wellenlänge, z.B. 2.2 µm?

Es ist wichtig zu beachten, dass die Korrektur großer räumlicher Skalen, insbesondere Tilt, sich auch auf kleine räumliche Skalen auswirkt, da Wellenfrontverkippungen kompensiert und somit flach werden. Übertragen auf die Strukturfunktion bedeutet dies, dass 		bei kleiner werdender Amplitude der Strukturfunktion die OTF Amplitude größer und die PSF entsprechend schmäler wird. Die Breite des Halos P' wird kleiner als die Breite der Seeing-begrenzten PSF. Die Verbesserung in der Halbwertsbreite FWHM kann einen Faktor 2-3 erreichen. Solche Adaptiven Optiken, die beispielsweise nur die Bildbewegung (Tilt) und Fokus korrigieren, werden als low-order Adaptive Optiken bezeichnete. Die damit erreichbaren Strehl-Zahlen sind in der Regel sehr klein, dennoch sind Verbesserungen in der Winkelauflösung um einen Faktor 2-3, gerade auch im sichtbaren Spektralbereich, immer wünschenswert und wissenschaftlich interessant.
Abbildung links (entnommen aus Roddier Buch 1. Auflage, Abb. 3.2) zeigt im doppel-logarithmischen Maßstab den Gewinn an Winkelauflösung (normalisierte Winkelauflösung) im Verhältnis zur Seeing-begrenzten Winkelauflösung als Funktion von \( D/r_0 \). Die durchgezogenen Kurven zeigen die Verbesserung bei einer perfekten Korrektur von jeweils
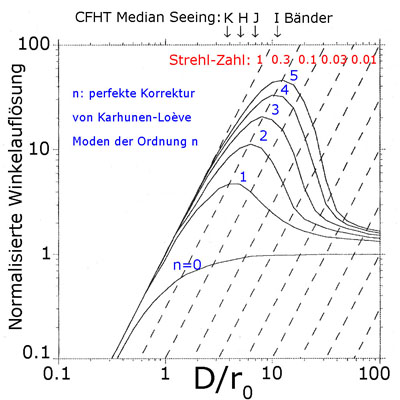
N = (n+1)(n+2)/2 Karhunen-Loève Moden (sehr ähnliche Kurven ergeben sich bei der Verwendung von Zernike Moden). Die gestrichelten Linien sind Linien gleicher Strehl-Zahl.

Die Kurve mit n=0 zeigt den Fall unkorrigierter Bilder. Die Winkelauflösung für kleine \( D/r_0 \) erreicht die Beugungsgrenze; für große \( D/r_0 \) nähert sich die Winkelauflösung asymtotisch dem (auf 1 normierten) Seeing. Die Kurve mit n=1 zeigt den Winkelauflösungsgewinn wenn die Karhunen-Loève Tip- und Tiltmoden perfekt korrigiert werden. Bei n=2 kommen noch die Moden Defokus und Astigmatismus hinzu. Alle Kurven haben ein Maximum bei einer Strehl-Zahl von ca. 0.3. An dieser Stelle ist die Adaptive Optik am effektivsten.

Für das 3.6-m Teleskop CFHT zeigen die Pfeile oben auf den Median Seeingwert für Beobachtungen im K, H, J und I-Band. Für das K-Band ist r0 hier etwas kleiner als 1m, was einem sehr guten Seeing entspricht.
Segmentierte deformierbare Spiegel mit Piezo-Stack Aktuatoren
Die ersten deformierbaren Spiegel, DM (deformable mirror), bestanden aus einzelnen, diskreten Elementen, die durch sehr kleine Lücken getrennt waren. Jedes Element wird entweder von einem Aktuator (siehe obiges Bild) kontrolliert (hoch und runter; Pistonkontrolle) oder von drei Aktuatoren (hoch und runter, Verkippung auf zwei Achsen; Piston- und Tip/Tilt-Kontrolle). Die Adaptive Optik NAOMI des William Herschel-Teleskops auf La Palma benutzt einen segmentierten Spiegel (siehe linkes Bild) mit 76 Piston- und Tip/Tilt-Aktuatoren (insgesamt 3*76=228 Piezo-Aktuatoren). Jedes quadratische Segment hat einen Durchmesser von 7.6mm. Etwa 2% des einfallenden Lichts wird aufgrund der Lücken nicht reflektiert.
Kontinuierliche deformierbare Spiegel mit Piezo-Stack Aktuatoren
Heutzutage benutzt die Standard Adaptive Optik an modernen Großteleskopen kontinuierliche deformierbare Spiegel. Dabei werden Piezo-Stack-Aktuatoren an eine dünne (deformierbare!) Glasplatte (continuous facesheet) angeklebt (siehe linkes Bild) und auf einer Referenzplatte ausgerichtet. Die Dicke der Glasplatte beeinflusst die so genannte Einflussfunktion (influence function), also die Form der Glasplatte wenn allein ein bestimmter Aktuator die Glasplatte herausdrückt. Die Glasplatte muss eine bestimmte Dicke haben, damit sie mit einer optischen Qualität besser als 1/10 der Arbeitswellenlänge poliert werden kann.
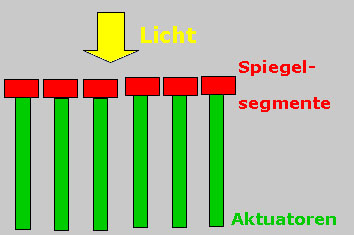
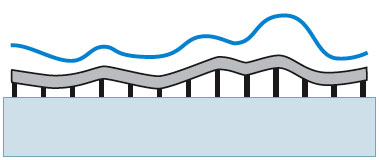
Typische Parameter segmentierter und kontinuierlicher Spiegel mit Piezo-Stack-Aktuatoren:

Anzahl Aktuatoren (nicht Segmente):
Abstand zwischen 2 Aktuatoren:
Aktuatorenanordnung:
Betriebsspannung:
Aktuatorhub:
Resonanzfrequenz:
Kosten:



100 - 1536 (3x512)
2-10 mm
rechteckige oder hexagonale Geometrie
einige 100 Volt
einige Mikrometer
einige kHz
hoch (ca. 1000 € pro Kanal)
Legt man an den Aktuator Nr. i die Spannung Vi an, lässt sich die Form des Spiegels beschreiben durch die Einflussfunktion ri(x,y) multipliziert mit der Spannung Vi. Sie ähnelt einer Glocken- (oder Gauss-) Funktion für kontinuierliche deformierbare Spiegel. Zwischen den einzelnen Aktuatoren gibt es in der Regel ein Übersprechen in der Größenordnung von 15%. Werden alle Aktuatoren angesteuert ist die Form des deformierbaren Spiegels gleich: \[ r(x,y) = \sum_i V_ir_i(x,y). \hspace{1cm} (3) \] Deformierbare Spiegel werden über Vielkanal Hochspannungsverstärker angesteuert. Die Ansprechzeit der Aktuatoren soll in der Regel so kurz wie möglich sein (<1ms) um die Korrekturbandbreite der Adaptiven Optik nicht zu reduzieren. Piezoaktuatoren mit elektrischen Kapazitäten um C=1µF und einem effektiven Widerstand von z.B. R=200 Ohm haben Zeitkonstanten von RC=200µs. Details über die dynamischen Eigenschaften von Piezoaktuatoren sind in englischer Sprache hier (pdf file, 200 KB) zusammengefasst. Die Bilder unten zeigen einen deformierbaren Spiegel der Fa. Xinetics mit 349 Aktuatoren (links die Vorderseite und rechts die Rückseite mit Anschlusssteckern und Flachbandkabeln). Die Verkabelung mit 2*349 Einzelkontakten (Masse und Signal) ist aufwendig.
349-Aktuator Spiegel
Anschlussseite

Zur sicheren Ansteuerung eines solchen Spiegels kann beispielsweise eine Elektronik der Fa. Cambridge Innovations eingesetzt werden (siehe nächstes Bild unten rechts). Diese schaltet zwischen Spiegel und Elektronik noch ein so genanntes TVS (Transition Voltage Suppression) Panel (siehe nächstes Bild unten links), welches den Spiegel vor Kurzschlüssen und zu hohen Spannungsdifferenzen (entsprechend lokal zu hohen mechanischen Belastungen) zwischen benachbarten Aktuatoren schützt.


Schutzplatine für einen 349-Aktuator Spiegel


Ansteuerelektronik für einen 349-Aktuator Spiegel
Bimorphe deformierbare Spiegel

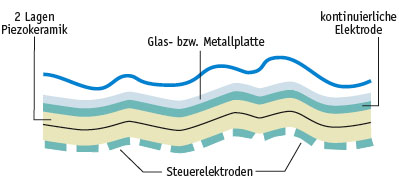
Schematischer Aufbau eines bimorphen Spiegels

Bimorphe deformierbare Spiegel bestehen aus einer dünnen Glasplatte, die direkt mit einer aus zwei Lagen bestehenden Piezo-keramikplatte verbunden ist. An den Ecken werden beide Platten so eingefasst, dass die Resonanzeigenschaften ähnlich der Membran einer gespannten Trommel sind. Die Verbindung zwischen Glas- und Piezokeramik enthält eine elektrisch leitfähige Elektrode und die Rückseite der Piezokeramik ist mit Steuerelektroden versehen, die von einander unabhängig sind. Legt man an diese eine elektrische Spannung an, so entstehen in der Piezokeramik seitwärts gerichtete (laterale) Kräfte, die zu einer Verbiegung des Spiegels führen. Dies rührt daher, dass die Piezokeramikplatte aus zwei entgegengesetzt polarisierten Piezolagen (wafer) besteht. Diese Konfiguration wird als serial bimorph bezeichnet. Wird eine Spannung angelegt, expandiert die eine Lage und die andere kontrahiert lateral. Das Ergebnis ist eine Verbiegung der Oberfläche.
Der Krümmungsradius R ist proportional zum Quadrat der Dicke h der Piezokeramik und umgekehrt proportional zur angelegten Spannung, also R ~ h2/V. Der lokale Hub des Spiegels S hängt von R und vom Quadrat des Durchmessers der Steuerelektrode d ab. Es gilt also S ~ d2/R. Die Resonanzfrequenz fR ist proportional zu h und umgekehrt proportional zum Spiegeldurchmesser D, also fR ~ h/D2.Diese drei Eigenschaften bimorpher Spiegel schränken die astronomische Anwendung auf Adaptive Optiken niedriger Ordnung ein. Will man die Anzahl von Aktuatoren (Elektroden) erhöhen, ohne die Resonanzfrequenz zu verändern, müsste der Spiegeldurchmesser kleiner werden um den gleichen Korrekturhub  zu erreichen. Der kleinste Spiegeldurchmesser wird aber durch eine Mindestdicke der Glasplatte eingeschränkt, denn diese ist zum Polieren und Kontaktieren nötig. Aus diesem Grund gibt es zur Zeit keine bimorphen Spiegel im Einsatz mit mehr als 100 Aktuatoren. Bimorphe Spiegel werden oft zusammen mit Curvature Wellenfrontsensoren eingesetzt.
Die Geometrie der Elektrodenanordnung für bimorphe Spiegel ist typischerweise eine radiale Ringstruktur (rechtes oberes Bild: die Elektrodenkonfiguration für den 60-Aktuator bimorphen Spiegel der adaptiven Optik MACAO des VLT). Diese Anordnung passt ideal zu runden Teleskopspiegeln mit ebenfalls runder Zentralschattung. Bimorphe Spiegel erreichen mit solch einer Geometrie - für eine gegebene Anzahl von Steuerelektroden (Aktuatoren) - die effizienteste Turbulenzkorrektur.

Die Spiegelform als Funktion der an die Elektroden angelegten Spannungen findet man über die Poisson-Gleichung. Diese beschreibt ganz allgemein (siehe unteres Bild) die Deformation einer dünnen Membran auf die Kräfte wirken.
Um die Poisson-Gleichung zu lösen müssen die Randbedingungen spezifiziert werden. Tatsächlich sind bimorphe Spiegel größer als der Strahldurchmesser; ein äußerer Ring von Elektroden bestimmt die Randbedingungen - Kontrolle von Wellenfrontneigungen an der Peripherie. Die Spiegelform lässt sich im statischen Fall durch \[ \nabla^2 (\nabla^2 r +AV ) = 0 \hspace{1cm} (4) \] beschreiben. \( \nabla^2 \) ist der zweidimensionale Laplace-Operator, r(x,y) die Spiegelform, V(x,y) die örtliche Spannungsverteilung, und A = 8d31 / t2. Hier bezeichnet t die Dicke der Piezoschicht und d31 den transversalen piezoelektrischen Koeffizienten.
Elektrodenanordnung des MACAO bimorphen Spiegels.

Bimorpher Spiegel mit angeschlossenen Elektroden.
Wechselt man in den Fourierraum - der Laplace-Operator entspricht einer Multiplikation mit \( |\vec{f}|^{2} \) - gilt für die entsprechenden Fourierkomponenten: \[ \vec{r}(\vec{f}) \propto |\vec{f}|^{-2} \tilde{V}(\vec{f}) \hspace{1cm} (5) \] Diese Gleichung beschreibt das Spektrum der Spiegelverformungen (Spiegelverbiegungen) in Abhängigkeit vom räumlichen Spektrum der Spannungen. Interessanterweise fällt das Spektrum mit f-2.
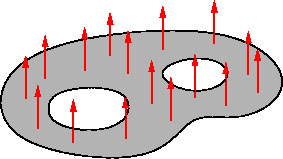
Dieses Verhalten ähnelt stark dem Kolmogorov-Spektrum der Phasenfluktuationen, welche mit f-11/6 fallen. Bimorphe Spiegel sind somit sehr gut geeignet Kolmogorov-ähnliche Turbulenz nachzubilden. 		Frage: Bei sehr starker Turbulenz kann der bimorphe Spiegel in die Sättigung gehen. Wird diese Sättigung zuerst bei großen oder kleinen Raumfrequenzen auftreten? Ist dies beim segmentierten Spiegel ähnlich?

Die mechanische Fixierung eines bimorphen Spiegels ist diffizil: einmal muss er sich biegen können zum anderen muss der Spiegel im gesamten optischen Strahlengang fixiert werden. Dazu kann der Spiegel beispielsweise mit drei V-förmig ausgeschnittenen Halterungen an den Rändern "fixiert" werden.

Bimorphe Spiegel wurden auf Anregung von François Roddier für astronomische Anwendungen entwickelt. Auch als billige Alternative zu Piezostack-Spiegeln. Bimorphe Spiegel werden in den Adaptiven Optiken einiger Teleskope (z.B. CFHT, SUBARU, GEMINI-NORD, ESO-VLTI, ESO-VLT) eingesetzt. Einziger Nachteil ist die im Vergleich zu Piezo-Stack deformierbaren Spiegeln deutlich geringere Zahl der Aktuatoren.
Typische Parameter bimorpher Spiegel:

Anzahl Aktuatoren:
Spiegeldurchmesser:
Aktuatorenanordnung:
Betriebsspannung:
Resonanzfrequenz:
Kosten:

13 - 188 (am SUBARU Teleskop)
30 - 200 mm
ringförmig, radial
einige 100 Volt
größer als 500 Hz
moderat
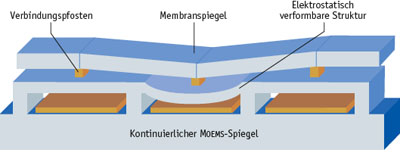
Deformierbare Spiegel auf MEMS bzw. MOEMS Basis
Seit einigen Jahren - in etwa seit Anfang der 1990er Jahre - gibt es ein Verfahren zur Herstellung deformierbarer Spiegel mit einer sehr großen Anzahl von Aktuatoren (Eintausend bis zehn Millionen), das auch recht preiswert ist. Es basiert auf einer Technologie, die MEMS (Micro-electro-mechanical systems) oder MOEMS (Micro-optical-electro-mechanical systems) genannt wird. Darunter fällt auch der von Texas Instruments Anfang der 1980er Jahre entwickelte und heutzutage in vielen Projektoren eingesetzte Digital Light Processor (DLP).
MOEMS werden mit Produktionstechniken** aus der Halbleitertechnologie hergestellt. Ihre Aktuatoren werden über elektrostatische Kräfte bewegt.

Die Abbildung rechts zeigt das Funktionsprinzip. Eine Elektrode wird gegenüber einer Maske aus einzeln ansteuerbaren Elektroden ange-bracht. Die elektrostatische Anziehung und Abstoßung zwischen den Elektroden führt zu Verformungen. 		**Während auf der Oberfläche von Wafern Halbleiter mit Hilfe der Photolithographie gefertigt werden, werden bei MEMS-spezifischen Verfahren z.B. Opferschichten und Strukturschichten (sacrificial and structural layers) auf die Wafer aufgebracht und mit Hilfe der Photolithographie durch selektives entfernen die gewünschten mechanischen Strukturen hergestellt. Dieses Verfahren wird als Surface Micromachining bezeichnet. MEMS Bauteile haben oft auch Strukturen auf beiden Seiten des Wafers.
Es gibt prinzipiell zwei mögliche Implementierungen. Entweder ist die Elektrodenmaske unbeweglich und die gegenüberliegende Elektrode bewegt sich, oder umgekehrt. Im letzten Fall kann die bewegliche Elektrode direkt mit einem reflektierenden Material beschichtet werden – und fertig ist der deformierbare Spiegel! Im ersten Fall kann eine beschichtete dünne Glasplatte an die Einzelelektroden kontaktiert werden, und man erhält ein MOEMS ähnlich einem Piezo-Stack-Spiegel. Eine weitere Möglichkeit ist in der Abbildung rechs angedeutet. Der typische Abstand zweier Aktuatoren eines MOEMS liegt bei etwa 100 Mikrometern. Allerdings ist der erreichbare Korrekturhub bei den heutzutage verfügbaren MOEMS-Spiegeln für die Anwendungen in der Astronomie noch nicht ausreichend. Ähnliches gilt für die optische Qualität der Spiegeloberflächen. Diese Probleme werden vermutlich in näherer Zukunft gelöst werden.
Deformierbare Spiegel auf Schwingspulen (Voice-coil) Basis - Adaptive Sekundärspiegel
Alle bisher erwähnten deformierbaren Spiegel werden in der Astronomie typischerweise optisch an den Ausgang des Teleskops gekoppelt (tertiäre Spiegel). Ein Adaptiver Sekundärspiegel unterscheidet sich von den vorher erwähnten in mancherlei Hinsicht. Die wesentliche Idee besteht darin, den Sekundärspiegel des Teleskops durch einen deformierbaren Spiegel zu ersetzen. Mit dieser Lösung reduziert man zum einen die Anzahl reflektierender Flächen bis zum Detektor. Dadurch wird die Transmission des Gesamtsystems erhöht. Zum anderen reduziert man die instrumentell bedingte thermische Hintergrundstrahlung. Ein weiterer Vorteil eines adaptiven Sekundärspiegels ist, dass dadurch alle Teleskopfoki von der Adaptiven Optik profitieren.

Ein erster adaptiver Sekundärspiegel wurde am Arcetri-Observatorium in Florenz entwickelt und im Jahr 2002 erstmals am 6.5-m-MMT-Teleskop auf dem Mount Lemmon in Arizona (USA) in Betrieb genommen. Das Bild rechts zeigt den adaptiven Sekundärspiegel montiert am Frontring des MMT-Teleskops.

Als Aktuatoren werden so genannte Voice-coils (ähnlich Lautspre-cherspulen) eingesetzt, die eine 50 mm dicke Basisplattform mit einer 1.8 mm dünnen, verformbaren, konvexen Glasplatte verbinden (siehe Bild rechts, unten). Zwischen Glasplatte und Basis-plattform befindet sich eine Referenzplatte, in die Löcher eingelassen sind. Darin befinden sich die Spulen-Aktuatoren. Kapazitive Abstandssensoren auf der Referenzplatte halten die Glasplatte, beziehungsweise die darin eingeklebten Magnete, auf dem gewünschten axialen Abstand. Die Luft zwischen Referenz- und Glasplatte wirkt dabei dämpfend. Mit Hilfe der Abstandssensoren und einer Regelschleife wird die Glasplatte unabhängig von der Teleskopstellung immer in der bestmöglichen Grundform gehalten.

Der MMT-Spiegel hat 336 Aktuatoren mit einem Aktuatorhub von etwa 100 Mikrometern und wird von 168 DSPs kontrolliert. Der Abstand zwischen zwei Aktuatoren liegt bei einigen Zentimetern (siehe Abbildung rechts). Damit lassen sich bei den typischen Größen von Sekundärspiegeln bis zu etwa 1000 Aktuatoren realisieren. Für das Large Binocular Telescope wird ein adaptiver Sekundärspiegel mit 672 Aktuatoren zum Einsatz kommen.Die Schwierigkeiten bei der Verwendung dieser Technik liegen einmal mehr bei möglichen Resonanzen zwischen Glasplatte und Aktuatorspulen, zwischen denen sich eine dämpfend wirkende dünne Luftschicht befindet. Nur durch ausgeklügelte Kontrollalgorithmen sind diese Resonanzen kontrollierbar. Weiterhin erreichen die Voice-coils die gewünschte Position erst nach mehr als einer Millisekunde, im Vergleich zu anderen deformierbaren Spiegeltypen recht langsam.

Bisher handelt es sich bei dieser Art Spiegel noch um Einzelstücke, so dass die Kosten dafür sehr hoch sind.

Nach adaptiven Tertiär- und Sekundärspiegeln stellt sich die Frage nach adaptiven Primärspiegeln von Teleskopen. Auch diese gibt es bereits wie am Beispiel des PAMELA Teleskops (siehe Bild unten) demonstriert wurde.

Der bedampfte adaptive Sekundärspiegel montiert am Frontring des
6.5-m MMT-Teleskops in Arizona (USA). (Foto: Laird Close, Steward Observatory, Arizona).

Der adaptive Sekundärspiegel des MMT mit 336 Voice-coil Aktuatoren. Der Spiegel hat einen Durchmesser von 64 cm. Die durchsichtige, 1.8 mm dünne Glasplatte ist noch nicht bedampft. Die dunklen Punkte sind auf der Rückseite der Glasplatte aufgeklebte Magnete, die von den Voice-coil-Aktuatoren (längliche Zylinder im Abstand von ca. 30 Mikrometern zu den Magneten) von der Referenzplatte weggedrückt werden können.

Bild links: das Pamela Teleskop mit adaptivem Primärspiegel bestehend aus 36 hexagonalen Tip-tilt und Piston-Spiegeln mit Voice-coil-Aktuatoren. Link zur englischsprachigen Webseite (Snapshot aus dem Jahr 2013): Pamela Webseite (2013).
Die Regelschleife (servo loop, control loop)
Eine aktivierte Adaptive Optik arbeitet in einer Regelschleife. Der Wellenfrontsensor misst die korrigierte optische Qualität (Wellenfront), vergleicht sie mit der gewünschten, idealen Wellenfront und steuert mit dem Differenzsignal den deformierbaren Spiegel. Durch diese Art der Regelung mit Rückmeldung (feedback) spielen Effekte wie Hysterese des deformierbaren Spiegels oder statische, optische Aberrationen im System so gut wie keine Rolle: sie werden automatisch mit den atmosphärischen, optischen Störungen korrigiert.

Hier soll nun das zeitliche Verhalten einer solchen feedback (closed-loop) Regelschleife etwas genauer analysiert werden.



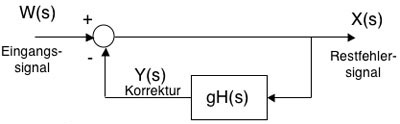
Jeweils Laplace transformiert (siehe Erklärung rechts) bezeichnen hier W(s) das Eingangssignal (z.B. der Koeffizient eines Zernike-Modes), Y(s) das Signal, welches an den deformierbaren Spiegel angelegt wird, und X(s) das Restfehlersignal wie es vom Wellenfrontsensor gemessen wird. Das Restfehlersignal muss durch einen Frequenzfilter H(s) laufen bevor es als Korrektursignal an den deformierbaren Spiegel angelegt wird. 		Die Laplace Transformation: In der Regelungstechnik treten häufig Zeitverläufe h(t) auf, die erst ab einem bestimmten Zeitpunkt t = 0 (Anfangszeitpunkt, z.B. bei Einschaltvorgängen in der Elektrotechnik) betrachtet werden. Berechnungen an derartigen Systemen führen in der Regel im Zeitbereich auf Differentialgleichungen. Um mit solchen Systemen einfacher rechnen zu können, wechselt man mit Hilfe der Laplace-Transformation in den Frequenzbereich (s ist dabei eine komplexe Größe, die komplexe Frequenz): \[ H(s) = \int_0^\infty h(t) e^{-st} dt \hspace{1cm} (6) \] \[ h(t) = \frac{1}{2\pi i} \int_{-i \infty}^{i \infty} H(s) e^{st} ds . \hspace{1cm} (7) \] In diesem Bereich treten statt der zeitabhängigen Differentialgleichungen nunmehr frequenzabhängige algebraische Gleichungen auf. Diese Gleichungen sind mit geringem Aufwand lösbar. Die gefundene Lösung muss allerdings wieder in den Zeitbereich rücktransformiert werden. Die Fourier Transformation kann als Spezialfall der Laplace Transformation betrachtet werden für reelle Frequenzen s=if.
Ohne eine solche Frequenzfilterung läuft die Regelschleife nicht stabil. Die Größe g bezeichnet die Verstärkung (gain) der Regelschleife.
H(s) heisst open-loop Übertragungsfunktion. Open-loop bedeutet in diesem Fall, dass kein Korrektursignal an den deformierbaren Spiegel angelegt wird.
Es gilt: Y(s) = X(s) g H(s) und X(s) = W(s) - Y(s).
Daraus folgt: X(s) = W(s) - g H(s) X(s) und somit: \[ X(s) = \frac{W(s)}{1 + gH(s)} \hspace{1cm} (8) \] und 		\[ Y(s) = \frac{gH(s)}{1+gH(s)} W(s) = T(s) W(s) \hspace{1cm} (9) \]

T(s) = gH(s)/(1+gH(s)) ist die closed-loop Übertragungsfunktion mit Verstärkungsfaktor g. Closed-loop bedeutet hier, dass das gefilterte Korrektursignal an den deformierbaren Spiegel angelegt wird. Im nächsten Zyklus (mit möglichst kleinem zeitlichen Abstand!) wird das aktuelle Eingangssignal mit dem "alten" Korrektursignal (feedback) korrigiert und ein neues Korrektursignal berechnet.


Regelkreis mit Integrator-Glied. Betragsquadrat der Error Rejection Transferfunktion als Funktion der Frequenz im doppellogarithmischen Maßstab. Störungen niedriger Frequenz werden am besten unterdrückt. Ab einer bestimmten Frequenz s=g, beträgt die Unterdrückung weniger als die Hälfte. Hohe Störfrequenzen werden nicht mehr kompensiert.

Einige Begriffe und Definitionen aus der Regeltechnik:

Servo: Gerät(e) zur Regelung. Beispiel: Servomotor.

Regelung: Kombination aus Messen und Steuern.

Steuerung: Eingangssignal und Ausgangssignal sind über ein oder mehrere Übertragungsglieder miteinander verbunden.

Open-loop: "Regelung" ohne Rückkopplung (Steuerung).

Closed-loop: Regelung mit Rückkopplung (feedback).

Open-loop Transferfunktion für reinen Integrator: H(s)=1/s.

Closed-loop Transferfunktion (Y(s)/W(s)): gH(s)/(1+gH(s)).

Closed-loop Error Rejection Transferfunktion (X(s)/W(s): 1/(1+gH(s)).

Sensitiviy: anderer Ausdruck für Error Rejection Transferfunktion.

0 dB Servo-Bandbreite in open-loop: für Frequenzen kleiner als die open-loop Bandbreite kann eine Verstärkung >1 (0 dB) angelegt werden. Höhere Frequenzen werden abgeschwächt, so dass keine Korrektur mehr erreicht werden kann.

0 dB Servo-Bandbreite der Fehlerunterdrückung (Error rejection) in closed-loop: für Frequenzen kleiner als diese Bandbreite werden Störungen unterdrückt. Für höhere Frequenzen werden Störungen erst verstärkt!!! und für noch höhere Frequenzen passiert dann nichts mehr.

-3 dB Servo-Bandbreite in closed-loop: definiert als die Frequenz bei der das Ausgangssignal X (oder die Verstärkung) auf die Hälfte des Wertes bei der Frequenz 0 gefallen ist. Dies ist die höchste definierte Bandbreite in Servoregelungen.

Bode Diagramm: graphische Darstellung einer komplexen Transfer-funktion. Ein Graph zeigt den Betrag der Transferfunktion (Gain) in Dezibel als Funktion der Frequenz, der andere den komplexen Wert der Transferfunktion (Phase) als Funktion der Frequenz. Die Frequenz-Achse ist dabei immer logarithmisch aufgetragen. Da Dezibel eine logarithmische Einheit ist, ist der Gain gegen Frequenz Graph doppellogarithmisch aufgetragen.

Beachte:
W(s), Y(s), X(s): Laplace Transformierte der Signale w(t), y(t), x(t) 		Eine Übertragungsfunktion kann beispielsweise nur aus einem Glied bestehen. Ist dieses Glied ein reiner Integrator sieht die zeitliche Funktionalbeziehung wie folgt aus:

\[ x(t) = g \int_{\tau=0}^{\tau=t} w(\tau)d\tau + x_0 \sigma(t) = x_1(t) + x_0 \hspace{1cm} (10) \] mit x0 als Anfangswert zur Zeit t=0. Die Stufenfunktion \( \sigma \) wirkt als Integrator auf das Eingangssignal, sie ist \( \sigma \)=0 für t<0 und \( \sigma \)=1 in allen anderen Fällen.
Laplace transformiert erhält man

X1(s) = gW(s)/s = gH(s)W(s) (11)

mit der open-loop Übertragungsfunktion H(s) = 1/s. Der Verstär-kungsfaktor g muss natürlich in den gleichen Einheiten wie die komplexe Frequenz s, also z.B. in Hz angegeben bzw. gemessen werden. Die closed-loop Übertragungsfunktion am Ausgang, TCL (Error rejection transfer function) nach Gl. (8), ergibt sich aus:

X(s) = W(s) / (1+g/s) = sW(s) / (s+g) = TCLW(s) (12)

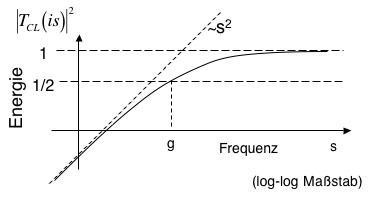
Für unendlich hohe Frequenzen is, \( i=\sqrt{-1} \), geht
TCL = s / (s+g) gegen 1 (Hochpassfilter) und im statischen Fall (is=0) gegen 0. Der Übergang vom Verhalten bei niedrigen Frequenzen zum Verhalten bei hohen Frequenzen liegt bei s=g. Die Unterdrückung der Signalenergie (power rejection) ist an dieser Stelle: \[ | T_{CL}(ig)|^2 = \frac{ig}{g+ig} \cdot \frac{-ig}{g-ig} = \frac{g^2}{2g^2} = \frac{1}{2} \hspace{1cm} (13) \] Beachte: Das Amplitudenquadrat einer elektromagnetischen Welle ist proportional zu dessen Energie.
Diese Frequenz s=g wird oft als Half-Power Frequenz bezeichnet. Betrachtet man nicht die Energie sondern nur den Betrag des Amplitudensignals, wird dieses an der Stelle s=g um den Faktor \( 1/\sqrt{2} \) = 1/1.41= 0.71 unterdrückt. Der Faktor 1.41 entspricht 3 dB, eine in der Signalverarbeitung (Nachrichtentechnik) gebräuchliche Angabe von Pegeln. Entsprechend wird die Frequenz is=g sehr oft auch mit f3dB bzw. als 3 dB Bandbreite bezeichnet, d.h. bis zu dieser Frequenz werden alle Eingangspegel um mindestens die Hälfte unterdrückt.

Beispiele für typische closed-loop Transferfunktionen Y/W und X/W adaptiver Optiken sind in den beiden untenstehenden Bildern gezeigt. Das rechte Bild, die Error Rejection Transferfunktion X/W, zeigt sehr anschaulich wie alle Störungen bis zu einer Frequenz von ca. 7 Hz unterdrückt werden. Störungen höherer Frequenz werden dann sogar verstärkt. Die 0 db Bandbreite liegt be ca. 7 Hz.

Im linken Bild ist die closed-loop Transferfunktion X/W als Funktion der Frequenz aufgetragen. Um die Stabilität der Regelschleife nicht zu gefährden, muss das Übersteuern (Gain > 0 dB) möglichst gering gehalten werden. Die -3 dB Bandbreite liegt bei ca. 18 Hz.

Beiden Graphen wurden für die Adaptive Optik Come-On berechnet, das erste (zivile) astronomische Adaptive Optik System, welches Anfang der 1990er Jahre auf dem La Silla Observatorium der ESO in Betrieb genommen wurde.
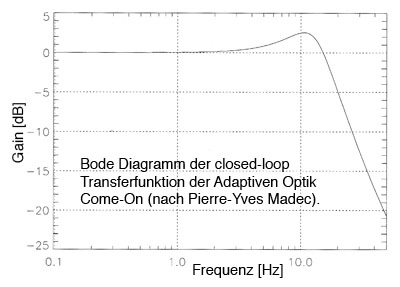Gain (Y(s) / W(s)) der closed-loop Transferfunktion der Adaptiven Optik Come-On (aus Roddier-Buch 1. Auflage, Seite 143). 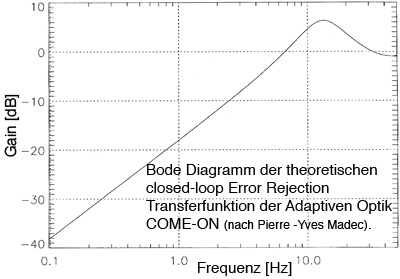Gain (X(s) / W(s)) der Error Rejection Transferfunktion der Adaptiven Optik Come-On (aus Roddier-Buch 1. Auflage, Seite 144).
Da atmosphärische, optische Turbulenz kleine Zeitkonstanten hat, muss natürlich das Korrekturelement (deformierbarer Spiegel) möglichst schnell angesprochen werden. Dabei sind 2 störende Punkte zu beachten:

1. Die Reaktionszeit des gesamten Systems. Die Messung der Wellenfront mit dem Wellenfrontsensor dauert eine bestimmte Zeit. Aus den Messdaten muss die Wellenfront rekonstruiert werden. Auch dies verbraucht Computerzeit. Ist die Wellenfront bestimmt wird daraus ein Korrektursignal für den deformierbaren Spiegel berechnet und an den Spiegel angelegt. Der Spiegel selbst braucht eine gewisse Zeit um die angelegten Spannungen in Verformungen umzusetzen. Im System gibt es somit einfache Verzögerungen (delays) als auch langsame Änderungen (lags) hin zum gewünschten Endzustand (Aktuator dehnt sich "langsam" aus). Je höher die zu kontrollierenden Frequenzen sind, um so kritischer wird die Reaktionszeit. Im Extremfall werden die Störungen nur noch verstärkt und das System wird instabil.

2. Rauschquellen. Schon die Messung der Wellenfront ist mit einem Fehler behaftet. In Abhängigkeit von der Helligkeit des Leitsterns der Adaptiven Optik und der Auslesegeschwindigkeit des 		Wellenfrontsensors erhält man unterschiedliche Signal-zu-Rausch-Verhältnisse. Der Verstärkungsfaktor bzw. die Bandbreite muss diesem Signal-zu-Rausch-Verhältnis angepasst werden. Dies ist kein einfacher Prozess, da hier verschiedene Faktoren zusammenspielen.

Digitale Servo-Kontroller tasten Signale nicht kontinuierlich sondern nur mit einer bestimmten Frequenz, der Schleifenfrequenz (loop frequency), ab. Solche digitalen Kontroller müssen in der Praxis deutlich schneller sein als das Nyquist-Shannon-Abtasttheorem sagt. Für die adaptive Optik gilt, dass die Schleifenfrequenz etwa 10-15fach höher sein muss als die 0 dB Servo-Bandbreite der Fehlerunterdrückung (siehe oben).

Frage: Falls die closed-loop Bandbreite halbiert werden soll, wie muss dazu der Verstärkungsfaktor im Kontrollsystem mit einem Integratorglied geändert werden?

Frage: Um welchen Faktor wird eine statische Störung/Aberration reduziert wenn eine Kontrollsystem mit einem Integratorglied eingesetzt wird?

Frage: Versuche die closed-loop Error Rejection Transferfunktion zu berechnen für einen Integrator mit Verzögerung. Was lässt sich über die Stabilität der Kontrollschleife sagen?
Restfehler kompensierter Wellenfronten
Ein deformierbarer Spiegel kann eine durch die atmosphäre gestörte Wellenfront nicht perfekt korrigieren. Zum einen besitzt er nur eine begrenzte Anzahl an Aktuatoren (räumlicher Fehler) zum anderen ist die Reaktionszeit nicht unendlich schnell (zeitlicher Fehler).

Der räumliche Fehler lässt sich durch den als konstant angenommenen Abstand zwischen zwei Aktuatoren d bestimmen. Dieser so genannte Fitting-Fehler der Phasenvarianz ist:

\[ \sigma_{fit}^2 = k \left ( d/r_0 \right )^{5/3} \hspace{1cm} (14) \]
mit dem Friedparameter r0 und einem vom Spiegeltyp abhängigen Faktor k. Für kontinuierliche Piezo-Stack Spiegel ist k=0.3. Die Gesamtzahl kontrollierter Aktuatoren in einem Teleskop mit Spiegeldurchmesser D ist proportional zu N = (D/d)2. Damit ergibt sich der Fitting-Fehler zu:

\[ \sigma_{fit}^2 = k \left ( D/r_0 \right )^{5/3} N^{-5/6} \hspace{1cm} (15) \] Könnte der deformierbare Spiegel N Zernike-Moden exakt darstellen, wäre der Fitting-Fehler durch die asymtotische Noll-Formel entsprechend Gl. 20 aus dem vorherigen Kapitel bestimmt.

Der Exponent in Nolls Formel ist \( -\sqrt{3}/2 \approx -0.866 \), verglichen mit -5/6 = 0.833 aus Gl. (15) keine sehr große Abweichung. Für große N ist eine Korrektur mit Zernike-Moden aber besser als eine lokale Korrektur über einzelne Aktuatoren. Dies ist mit ein Grund für die größere Effizienz bimorpher Spiegel im Vergleich zu Piezo-Stack Spiegeln. Bimorphe Spiegel können Zernike-Moden exakter darstellen bzw. reproduzieren. 		Für den zeitlichen Fehler kann man zeigen, dass die so genannte Servo-Bandbreite Phasenvarianz durch: \[ \sigma_{servo}^2= (\tau_0 f_{3dB})^{-5/3} \hspace{1cm} (16) \] charakterisiert ist. \( \tau_0 \) ist die atmosphärische Zeitkonstante, f3 dB die 3 dB closed-loop Bandbreite, die in etwa dreimal so hoch ist wie die 0 dB Servo-Bandbreite der Fehlerunterdrückung (siehe oben). Der Kehrwert von \( \tau_0 \) wird Greenwoodfrequenz genannt.

Tatsächlich hängt das zeitliche Spektrum der Zernike-Koeffizienten von der Ordnung des Zernike-Modes ab: Moden niedriger Ordnung ändern sich zeitlich langsamer als Moden höherer Ordnung. Es wäre also vernünftig, jeden Mode mit einer eigenen Antwortzeit zu kontrollieren um so den verbleibenden Phasenfehler zu optimieren bzw. zu minimieren; insbesondere wenn die Wellenfrontmessung hohe Rauschanteile hat. Viele Adaptive Optiken in der Astronomie benutzen eine Modenkontrolle; neben Zernike- und Karhunen-Loève Moden werden auch an die Hardware angepasste Moden (Spiegelmoden) verwendet.

Frage: Wenn allein die Regelbandbreite der Regelschleife betrachtet wird und bei einer atmosphärischen Zeitkonstanten von \( \tau_0 \) =4 ms eine Strehl-Zahl von 0.9 erreicht werden soll, wie hoch muss f3 dB sein?

Frage: Für ein 8-m Teleskop und einem Seeing von 1 Bogensekunde, berechne die Anzahl der Piezo-Stack-Aktuatoren um eine Strehl-Zahl von 0.37 bei einer Wellenlänge von 0.5 µm zu erhalten. Wieviele Zernike-Moden müssen kompensiert werden um die gleiche Strehl-Zahl zu erhalten?
Zusammenfassung dieses Kapitels
Die optische Qualität teilkompensierter Bildaufnahmen kann mittels der Strehlzahl bestimmt werden. Die Freiheitsgrade wie Anzahl Aktuatoren und Regelbandbreite können passend zur gewünschten Adaptiven Optik ausgewählt werden. Verschiedene Arten deformierbarer Spiegel wurden vorgestellt. Einige relevante Grundlagen der Regelungstechnik wurden erläutert. Wichtige Fehlerquellen, die zu verbleibenden Phasenfehlern führen, Fittingfehler und Servofehler, wurden eingeführt. Im nächsten Kapitel geht es um die Messung und Bestimmung/Rekonstruktion von Wellenfronten mit Hilfe von Wellenfrontsensoren.
nach oben                      vorheriges Kapitel                      nächstes Kapitel