|
Adaptive Optik Online mit Fokus auf die Astronomie
|

|
| |
|
Von Stefan Hippler und
Andrei Tokovinin
|
Heidelberg im Februar 2024
|
| |
Atmosphärische optische Turbulenz
Bildgebende Photometrie (Imaging) durch optische Turbulenz
|
zum Inhaltsverzeichnis von
Adaptive Optik Online
|
| |
|
Das Teleskop mit kreisrunder Apertur
|
| |
|
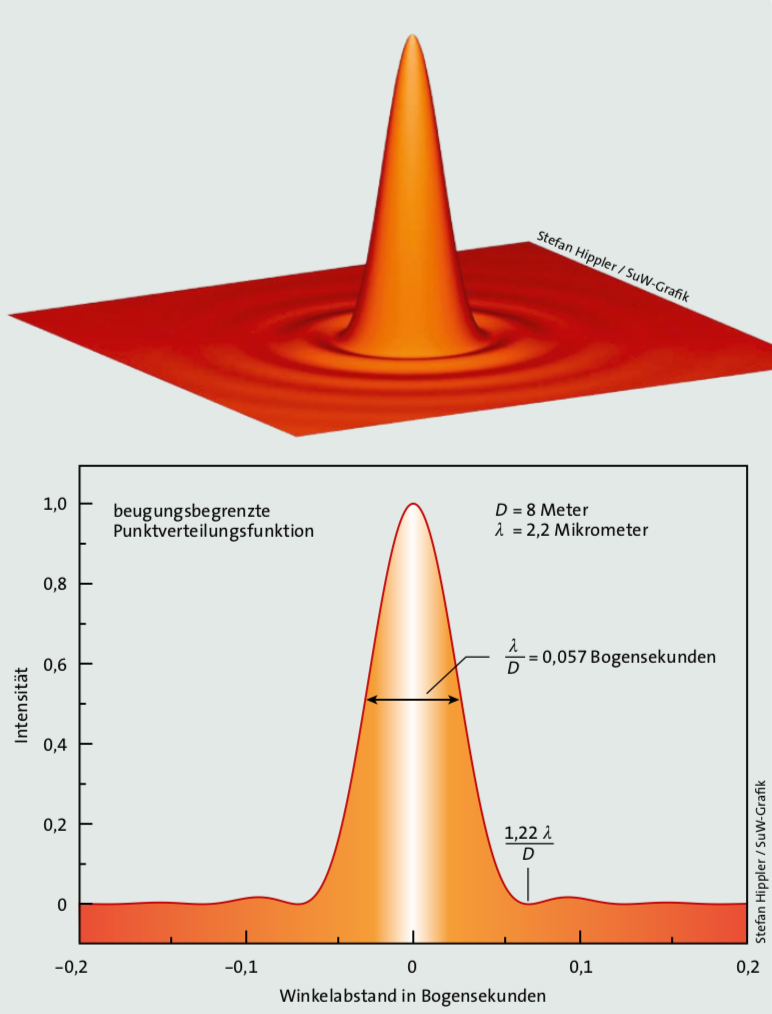
Das Bild einer Punktquelle (Stern), das mit einem Teleskop aufgenommen wird, ist durch
Beugungseffekte
bestimmt und läßt sich durch die Airy Funktion
\( P_0 \)
(Bild links oben: 3D Darstellung, darunter Plot eines Schnitts durch das Zentrum) mathematisch beschreiben:
\[
P_0(\vec{\alpha}) =
\frac{\pi D^2}{4\lambda^2}
\left[ \frac{2 J_1 ( \pi D |\vec{\alpha}| / \lambda )}{\pi D |\vec{\alpha}|/ \lambda} \right]^2 \hspace{1cm}
(1)
\]
dabei ist \( P_0 ( \vec{\alpha} ) \)
die Lichtintensität in der Fokalebene des Teleskops als Funktion der zweidimensionalen
Winkelkoordinate \( \vec{\alpha} \),
der Wellenlänge des Lichts λ,
dem Durchmesser des Teleskopspiegels D und der so genannten
Besselfunktion
J1.
Das erste Minimum (dunkler Ring) befindet sich in einem Winkelabstand von
1.22 λ/D zum Zentrum hin.
Dieser Abstand wird oft als ein Maß für die kleinste Winkelauflösung des Teleskops genommen.
Die Projektion der 3D Airyfunktion auf eine Ebene entspricht dem Bild einer beugungsbegrenzten Punktquelle auf einem Detektor.
Diesen "Punkt", in der Regel verteilt auf mehrere Pixel, bezeichnen Astronomen oft
als Beugungsscheibchen oder Airyscheibchen.
Ist der Punkt nicht beugungsbegrenzt wird in der bodengebundenen Astronomie von Seeing-Scheibchen gesprochen.
|
| |
| |
| |
|
Das Bild \( I ( \vec{\alpha} ) \)
eines astronomischen Objekts \( O ( \vec{\alpha} ) \)
lässt sich als Vielzahl von Punkten darstellen. Mathematisch wird es als Faltung (convolution)
der wahren Helligkeitsverteilung des Objekts mit der Punktverteilungsfunktion (PSF, Point Spread Function)
\( P_0 \) des Teleskops beschrieben: I = O * P mit dem Faltungsoperator *, der
einem Integral über den gesamten Raum entspricht:
\[
I(\vec{\alpha}) =
\int \int O( \vec{\alpha}^\prime) P_0 (\vec{\alpha} - \vec{\alpha}^\prime) d^2 \vec{\alpha}^\prime \hspace{1cm} (2)
\]
Gleichung (2) beschreibt also die Bildentstehung (image formation)
|
in einem Teleskop oder auch Mikroskop. Die beispielsweise von einem CCD gemessene Intensitätsverteilung
des Bildes \( I ( \vec{\alpha} ) \)
auf einem Pixel mit den Koordinaten \( \vec{\alpha} \),
ergibt sich als Beitrag aller Punkte des Objekts \( O ( \vec{\alpha} ) \)
mit ihren echten Intensitäten, gewichtet mit der verschobenen PSF \( P_0 \). Das Bild wird also im
Vergleich zum Objekt durch die PSF geglättet, was einer Verschlechterung der Winkelauflösung entspricht.
Man spricht von beugungsbegrenzter Abbildung. Ein Beispiel einer astronomischen Aufnahme des Milchstraßenzentrums
mit verschiedenen Winkelauflösungen zeigt das nächste Bild.
|
| |
| |
| |

Das Zentrum der Milchstrasse aufgenommen mit dem 3.6-m Teleskop CFHT
bei einer Wellenlänge von 2.2 Mikrometern. Die Winkelauflösung in der linken Aufnahme, ohne adaptive Optik, wird durch die atmosphärischen
Bedingungen, dem Seeing, bestimmt und ist mit 0.57 Bogensekunden ca. 4.4 mal so groß wie die mit adaptiver Optik erreichte Winkelauflösung
von 0.13 Bogensekunden.
|
| |
| |
| |
Frage:
Wie hängt die beugungsbegrenzte Winkelauflösung
von der Wellenlänge ab?
|
Aufgabe:
Berechne die beugungsbegrenzte Winkelauflösung des menschlichen Auges bei Tag und bei Nacht.
|
| |
|
Die Punktverteilungsfunktion (Point Spread Function, PSF)
|
| |
|
Das bisher gesagte galt für das ideale Teleskop. Kann das Teleskop nicht im Idealzustand
betrieben werden, dann ändert sich das Bild einer Punktquelle so, daß die Winkelauflösung
schlechter wird als durch die Airy Funktion gegeben. Gleichung (2) gilt weiterhin allerdings
mit einer anderen PSF \( P ( \vec{\alpha} ) \).
Die Breite der PSF ist ein Maß für die Winkelauflösung.
Hinweis 1: Implizit wurde angenommen
daß \( P ( \vec{\alpha} ) \)
das Bild eines Sterns mit Einheitsintensität ist, d.h. das Integral
von \( P ( \vec{\alpha} ) \) über
|
alle \( \vec{\alpha} \) ergibt 1. Gleichung (2)
konserviert den Gesamtfluß eines astronomischen Objekts, verteilt ihn aber unterschiedlich auf die einzelnen Pixel.
Hinweis 2: Es wurde angenommen, daß die PSF die gleiche Form über das gesamte Bildfeld besitzt.
Dieser Zustand wird als Isoplanarität (isoplanatism) bezeichnet. Die Isoplanarität ist insbesondere
bei der Benutzung einer Adaptiven Optik auf sehr kleine Bildfelder beschränkt; über größere Bildfelder
gibt es eine langsame Veränderung der PSF. In diesem Fall kann Gleichung (2) über kleinere Teile
des ganzen Bildfeldes angewandt werden.
|
|
Kriterien zur Winkelauflösung
|
| |
|
Die Form einer PSF kann irregulär sein; verschiedene numerische Größen für die Winkelauflösung finden dann Anwendung:
1. FWHM = Die Breite der PSF an der Stelle wo die Intensität 50% des Maximums beträgt (Full Width at Half Maximum).
2. Die Strehl-Zahl S, das Verhältnis der maximalen/zentralen Intensität der PSF zur maximalen/zentralen
Intensität der Airy Funktion; S=P(0)/P0(0). Je höher die Strehl-Zahl (maximal 1) um so besser ist
die Winkelauflösung. Von beugungsbegrenzter Auflösung spricht man wenn die Strehl-Zahl S>0.8 ist.
Auf dem Gebiet der adaptiven Optik wird auch bei deutlich kleineren Strehl-Zahlen von beugungsbegrenzter Auflösung
gesprochen und zwar dann, wenn die FWHM der PSF gleich der FWHM der Airy Funktion ist. Dabei sitzt in der Regel ein
kleiner Peak auf einem breiten Untergrund (Seeing Halo), eine Form deutlich unterschiedlich zur Airy Funktion.
|
3. Im Kreis eingeschlossene Energie (encircled energy) EE. Das Integral über die PSF ist
nach Definition 1. Das Integral der PSF über einen Kreis mit dem Durchmesser EED (encircled energy diameter) heißt
encircled energy EE.
Ist beispielsweise 50% der gesamten Energie im sichtbaren Spektralbereich eines Objekts
in einem Kreis mit Durchmesser von 0.5 Bogensekunden hat man sehr gute Beobachtungsbedingungen. Die EE ist
eine wichtige Kenngröße bei der Planung und Beobachtung sehr lichtschwacher Objekte, denn hier kommt es oft darauf
an möglichst viele Photonen auf einzelne Pixel zu verteilen um ein Signal über dem Rauschen zu erhalten.
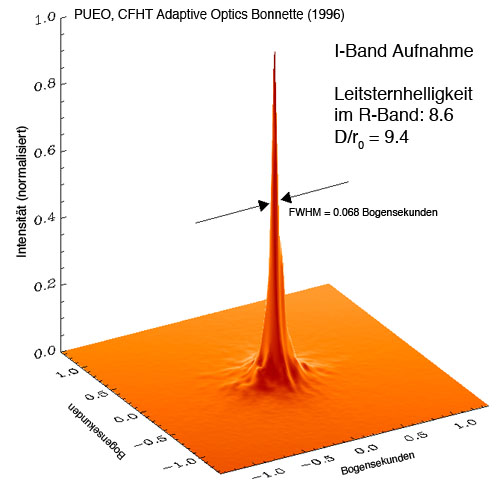
Das Beispiel einer am CFHT 3.6-m Teleskop gemessen PSF im I-Band (0.8µm) mit aktivierter Adaptiver
Optik (PUEO) zeigt das nächste Bild.
|
| |
| |
| |
| |
|
|
| |
| |
| |
Frage:
Wie ändert sich die Strehl-Zahl wenn die PSF im obigen Bild nur halb so breit wäre?
|
Frage:
Wie groß ist die Strehl-Zahl eines perfekten Teleskops bei der Wellenlänge
λ wenn eine Hälfte des Hauptspiegels um
λ/2
tiefer liegt als die andere Hälfte.
|
|
Die optische Übertragungsfunktion (optical transfer function, OTF)
|
| |
Die mathematische Beschreibung der Bildentstehung im Teleskop mit Hilfe des Integrals
aus Gleichung (2) läßt sich mit Hilfe der Fouriertransformation in eine einfache Multiplikation
umwandeln:
\[
\tilde{I}(\vec{f}) = \tilde{O}(\vec{f}) \cdot \tilde{P}(\vec{f}) \hspace{1cm} (3)
\]
In dieser Gleichung bezeichnet \( \vec{f} \)
die Raumfrequenz (wird \( \vec{\alpha} \) beispielsweise
in Radian gemessen, dann wird \( \vec{f} \)
in 1/Radian oder Zyklen pro Radian angegeben).
\( \tilde{P}(\vec{f}) \)
nennt man die optische Übertragungsfunktion OTF (optical transfer function) des Systems (Teleskops). Sie beschreibt die Änderung
der Modulation (Kontrast) und der Phase des fouriertransformierten Objekts \( \tilde{O}(\vec{f}) \)
im Prozess der Bildentstehung. Die OTF ist im allgemeinen eine komplexe Funktion.
Der Absolutbetrag der OTF heißt
Modulationsübertragungsfunktion (MTF, modulation transfer function). Allgemein gilt:
mit der Phasenübertragungsfunktion PTF. Da die OTF die Intensitätsverteilung des Objekts auf die des Bildes überträgt,
kann ihr Absolutbetrag nie größer als 1 sein, da keine Information aus dem Nichts heraus erzeugt werden kann.
|
Typischerweise fällt die MTF mit größer werdenden Raumfrequenzen. Dies führt in der Regel zu einer Abschwächung
von Details oder völligem Detailverlust im Bild.
Für jedes optische System gilt \( |\tilde{P}(\vec{f})| = 0 \) für
Raumfrequenzen größer einer bestimmten Abschneidefrequenz \( |\vec{f}| \ge f_c \).
Für ein Teleskop mit Spiegeldurchmesser D gilt fc = D/λ.
Dies bedeutet, dass Raumfrequenzen größer als fc nicht beobachtet werden können und nur größere Teleskope feinere Details
bzw. kleinere Objekte abbilden können.
Die Relation zwischen der PSF und der OTF ist durch die Fouriertransformation bestimmt. Kennt man die eine Funktion kennt man
auch die andere; die Information die beide Funktionen enthalten werden eben nur unterschiedlich dargestellt.
Weiterhin gilt \( \tilde{P}(0) = 1 \)
(vergleiche mit der PSF Normalisierung).
Die Strehl-Zahl ist proportional zum Integral der OTF über alle Raumfrequenzen.
Frage:
Was ist die Mindestgröße eines Teleskops, um einen Zaun mit 10 cm Lattenabstand aus einer Entfernung von 5 km aufzulösen?
|
|
Bildgebende Photometrie (imaging) durch optische Turbulenz bei langbelichteten Aufnahmen
|
|
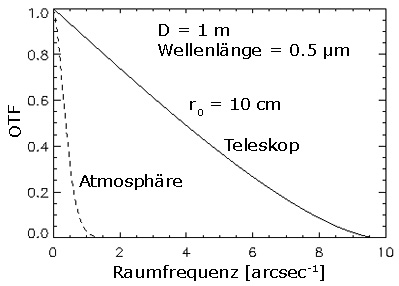
Atmosphärische optische Turbulenz lässt sich als statistische Phasenstörungen beschreiben,
welche die elektromagnetischen Wellen beim Durchlaufen der Atmosphäre erfahren.
Die Störungen oder Aberrationen
ändern sich kontinuierlich mit der Zeit. Gleiches gilt für die PSF. Betrachtet man die mittlere PSF, die
einer langbelichteten Aufnahme entspricht, gilt der folgende Zusammenhang:
\[ \tilde{P}_{LE} (\vec{f}) = \tilde{P}_0(\vec{f}) \cdot \tilde{P}_a(\vec{f}) \hspace{1cm} (5) \]
Die langbelichtete (Long Exposure) OTF, \( \tilde{P}_{LE} (\vec{f})\),
ist das Produkt der atmosphärischen Übertragungsfunktion \( \tilde{P}_{a} (\vec{f}) \)
und der OTF des Teleskops \( \tilde{P}_{0} (\vec{f}) \).
Für große Teleskope mit guter optischer Qualität ist die kleinste Winkelauflösung durch die Atmosphäre limitiert,
d.h. \( \tilde{P}_{0} (\vec{f}) = 1 \) und
\( \tilde{P}_{LE} (\vec{f}) \approx \tilde{P}_{a} (\vec{f}) \).
Durch Fouriertransformation von \( \tilde{P}_{LE} (\vec{f})\)
erhält man die langbelichtete PSF.
|
| |
| |
| |
|
Die atmosphärische OTF ist verknüpft mit der Statistik der atmosphärischen Phasenstörungen,
der so genannten Phasenstrukturfunktion
\( D_\phi(\vec{r}) \),
über:
\[
\tilde{P}_{a}(\vec{f}) =
\exp{[-0.5D_\phi(\lambda \vec{f})]} \hspace{1cm} (6)
\]
Hinweis:
In dieser Formel geht man über von dreidimensionalen Raumkoordinaten
\( \vec{r} \)
in der Ebene der Wellenfront auf Raumfrequenzen in der Bildebene multipliziert mit der Wellenlänge.
Diese Relation folgt aus der Wellenoptik: jede Fourierkomponente eines Bildes entsteht aus der Interferenz
von Lichtwellen, die um einen gewissen Abstand separiert sind. Dieses Prinzip gilt sowohl für Radio-
als auch optische Interferometer.
|
Frage:
Angenommen die Form der atmosphärischen PSF ist Gaußförmig (also sehr ähnlich dem natürlichen Seeing).
Wie sieht dann die entsprechende Strukturfunktion aus?
Frage:
Ist die Form der atmosphärischen PSF sensitiv in den Bereichen
\( D_\phi \gg 1 \)
und
\( D_\phi \ll 1 \) ?
|
| |
|
Statistik der atmosphärischen optischen Turbulenz
|
Die von der Atmosphäre gestörte Wellenfront kann man sich als ein unregelmäßig gewelltes/gebeultes (Berg- und Talstruktur)
Blatt Papier vorstellen.
Die von einem weit entfernten Objekt (Stern) ausgesandte elektromagnetische Welle
ist perfekt flach bevor sie in die Erdatmosphäre eintritt. Beim Durchlaufen der Atmosphäre treffen Teile der Welle
auf wärmere und andere Teile der Welle auf kältere Luft. Diese optisch dichteren (warm) und dünneren (kalt) Luftwirbel
verringern bzw. vergrößern auf Grund der unterschiedlichen Brechungsindizes die Lichtgeschwindigkeit der Welle in der Atmosphäre.
Das Resultat ist eine deformierte Wellenfront. Der Zweck der Adaptiven Optik besteht darin, diese Deformationen zu kompensieren.
Dazu ist es wichtig die optischen Störungen statistisch zu charakterisieren.
Die Luft ist für Wellenlängen λ > 500nm nur schwach dispersiv.
Dies wird hier nicht weiter beachtet und die Phasenstörungen - charakterisiert durch Änderungen der optischen Weglänge
\( l(\vec{x}) \)- achromatisch behandelt.
Dagegen ist die Phase der elektromagnetischen Welle natürlich Wellenlängenabhängig:
|
\[
\phi(\vec{x}) = \frac{2\pi}{\lambda} l(\vec{x}) \hspace{1cm} (7)
\]
Wir nehmen an, dass für die hier betrachteten statistischen Störungen (Phasenstörungen, Temperaturstörungen,
Druckstörungen) der jeweilige räumliche Mittelwert (durch eckige Klammern gekennzeichnet) Null
ist, also z.B. für die Phasenstörungen \( \langle\phi\rangle = 0 \) gilt.
Obwohl statistische Prozesse wie \( \phi(\vec{x}) \) oft
durch Korrelationsfunktionen oder
durch Kovarianzen beschrieben
werden, arbeitet man in der atmosphärischen Wissenschaft bevorzugt mit Strukturfunktionen.
Die Strukturfunktion D, ein
Konzept entwickelt von Andrei Kolmogorov 1941, beschreibt hier die räumlichen Eigenschaften des turbulenten Mediums.
Dies geschieht indem die mittlere Differenz des statistischen Prozesses
an zwei Orten bestimmt wird (hier für die Phasen \( \phi \)):
\[
D_\phi(\vec{r}) = \langle [ \phi(\vec{x}+\vec{r}) - \phi(\vec{x}) ]^2 \rangle \hspace{1cm} (8)
\]
|
| |
| |
| |
|
|
Frage:
Was ist der Zusammenhang zwischen Strukturfunktion und der Kovarianzfunktion
\( B(\vec{r}) = \langle \phi(\vec{x}+\vec{r}) \cdot \phi(\vec{x}) \rangle \)?
Frage:
Wie hängt die atmosphärische Strukturfunktion in Gleichung (8) von der Wellenlänge ab?
|
| |
| |
| |
| |
|
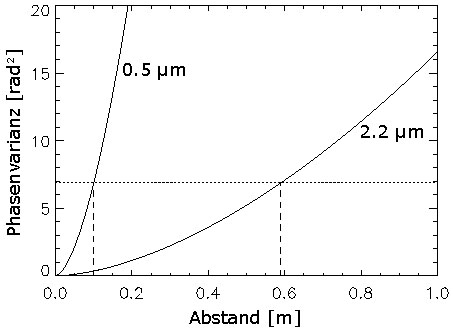
Die Phasenvarianz als Funktion des Abstandes für zwei verschiedene Wellenlängen.
|
Das Kolmogorov Modell der Turbulenz führt zu einer einfachen Relation
(von Valerian Illich Tatarskii)
zwischen der Phasenstrukturfunktion aus Gleichung (8) und einem einzigen Parameter, der so genannten Kohärenzlänge r0
auch Friedparameter genannt. Es gilt:
\[
D_\phi(\vec{r}) =
6.88\left(\frac{|\vec{r}|}{r_0}\right)^{5/3} \hspace{1cm} (9)
\]
Da die Pfadlänge achromatisch ist, folgt sofort dass \( r_0 \sim \lambda^{6/5} \)
ist.
Es ist daher wichtig bei Angaben von r0 immer die Wellenlänge mit anzugeben. Der Parameter r0 ist
eine griffige Messgröße, die die räumliche Stärke der Turbulenz charakterisiert. In diesem einen Parameter stecken
alle Brechungsindexvariationen der gesamten Atmosphäre. Kleine Werte von r0 entsprechen starker
Turbulenz, große Werte entsprechend schwacher Turbulenz und gutem Seeing.
|
Wenn nicht anders angegeben, gelten r0 Werte für eine Wellenlänge von 0.5µm.
Typische Werte von liegen bei 5-10 cm für Wellenlängen um 0.5 µm und bei 40-80 cm für Wellenlängen
um 3 µm. Eine weitere Interpretation von r0 ist, dass damit genau der Aperturdurchmesser
gegeben ist, in dem die Phasenänderungen kleiner 1 rad rms sind. Teleskope dieser Größe arbeiten in
etwa beugungsbegrenzt.
Das hier in aller Kürze zusammengefasste Modell ist - obwohl es sehr primitiv erscheint - die
Basis für die gesamte Theorie der Bildentstehung durch atmosphärische optische Turbulenz hindurch,
Adaptive Optik mit eingeschlossen. Das Kolmogorov Modell gilt nur in einem bestimmten, so genannten
Inertialbereich.
|
Dieser ist markiert durch einen kleinsten Abstand (inner scale) von wenigen
Millimetern und einem größten Abstand (outer scale) von mehreren Metern.
Frage:
Was ist das quadratische Mittel
(rms, root mean square) der atmosphärischen Phasendifferenz bei einem Abstand von r=r0 in Einheiten von
Radian und Wellenlängen?
Frage:
Wenn r0=15 cm groß ist bei einer Wellenlänge von 0.5 µm, wie groß ist dann r0 bei einer
Wellenlänge von 2.2 µm ?
|
| |
| |
| |
Setzt man nun die Phasenstrukturfunktion (Gl. 9) in die atmosphärische OTF (Gl. 6) ein erhält man:
\[
\tilde{P}_a(\vec{f}) =
\exp{[-3.44(\lambda | \vec{f} | /r_0)^{5/3}]} \hspace{1cm} (10)
\]
Die atmosphärische langbelichtete PSF ergibt sich dann durch eine Fouriertransformation von Gl. 10.
Erhält man eine Gauß-Funktion? Weiterhin erhält man einen Zusammenhang zwischen der Halbwertsbreite
(FWHM) der atmosphärischen PSF (auch als Seeing bezeichnet) und dem Friedparameter r0.
\[
\mathrm{FWHM} = 0.98 \frac{\lambda}{r_0} \hspace{1cm} (11)
\]
Gut zu merken ist, dass man bei einem Seeing von 1 Bogensekunde und einer Wellenlänge von 0.5µm
eine FWHM ein r0 von etwa 10 cm hat.
Wie bereits oben gesagt, ist die Strehl-Zahl der atmosphärischen PSF exakt die gleiche wie für ein
Teleskop mit Durchmesser r0 (daher der Koeffizient 6.88 in Gl. 9. Für ein großes
Teleskop mit einem Durchmesser D deutlich größer als r0, ist die Strehl-Zahl
einfach S = (r0/D)2.
Frage:
Wie groß ist die Strehl-Zahl einer langbelichteten Punktquelle an einem 4-m Teleskop
bei einem Seeing von 1 Bogensekunde bei 0.5 µm und 2.2 µm Wellenlänge?
|
Der Friedparameter r0 wird manchmal als charakteristische Länge (Kohärenzlänge, coherence length)
der atmosphärischen Störungen bezeichnet. Dies ist nicht ganz korrekt: man sieht, dass das
Kolmogorov (Leistungs-) Spektrum nur proportional zur Raumfrequenz f-5/3 ist.
Allerdings sind nur Störungen in der Größenordnung von r0 für die langbelichtete
Aufnahme relevant. Auf kleineren Skalenlängen sind die Störungen wesentlich kleiner als die
Wellenlänge und auf größeren Skalen wird \( D_\phi(\vec{r}) \)
so groß, dass die atmosphärische OTF null wird.
Die Stärke der turbulenten Fluktuationen des Brechungsindex in der Atmosphäre wird durch eine
Brechungsindex-Strukturkonstante \( C_n^2 \)
angegeben (das Quadrat zeigt hier wieder die mittlere quadratische Differenz wie in Gl. 8 an).
Die Einheit von \( C_n^2 \) ist m-2/3.
Die Abhängigkeit von \( C_n^2 \) von
der Höhe der Turbulenz über dem Boden gibt das Turbulenzprofil wieder. Das astronomische Seeing und
entsprechend Gl. 11 r0 hängen vom Integral des Turbulenzprofils wie folgt ab:
\[
r_0^{-5/3} = 0.423 (\frac{2\pi}{\lambda})^2 \sec{z} \int_0^{H_{max}} C_n^2 (h) \mathit{dh} \hspace{1cm} (12)
\]
wobei z die Zenitdistanz bezeichnet, h die Höhe über dem Boden und Hmax
die maximale Integrationshöhe der atmosphärischen Turbulenz (typischerweise ca. 20 km).
|
| |
| |
|
|
|
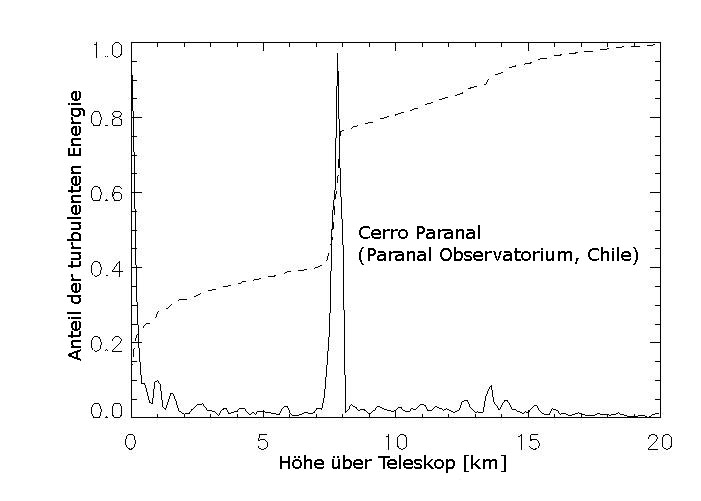
Beispiel eines Turbulenzprofils aufgenommen auf dem Cerro Paranal in Chile. Die durchgezogene
Linie zeigt \( C_n^2 \)
in relativen Einheiten. Der bis zur jeweiligen Höhe aufintegrierte Anteil ist durch die gestrichelte
Linie gezeigt (50% der gesamten turbulenten Energie liegt in diesem Plot knapp unterhalb von 8km).
Zu erkennen ist weiterhin, dass hier ein Großteil der gesamten optischen Turbulenz in zwei Schichten
konzentriert ist, eine Nahe dem Boden, die andere zwischen 7-8 km. Dennoch ist in etwa 1/3 der gesamten
Energie kontinuierlich über alle anderen Höhen verteilt.
Frage:
Wie hängen nach Gleichung (12) r0 und das Seeing von der Zenitdistanz ab.
|
|
Die atmosphärische Zeitkonstante
|
| |
|
|
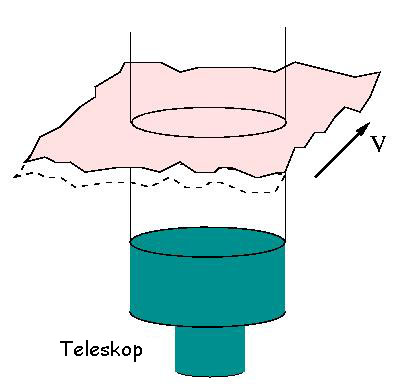
Optische Turbulenz lässt sich oft durch statische Phaseschirme mo-dellieren.
Diese werden mit einer Windgeschwindigkeit vw über das Teleskop geschoben.
Kennt man die räumlichen Eigenschaften dieser Phasenschirme (Strukturfunktion) und die
Windgeschwindigkeit vw, dann kennt man auch das zeitliche Verhalten wie es vom
Teleskop in einer Richtung beobachtet wird. Die atmosphärische Zeitkonstante ist definiert als
\[
\tau_0 = 0.31 \frac{r_0}{V} \hspace{1cm} (13)
\]
mit der über die Höhe gemittelten Windgeschwindigkeit V. Die Zeitkonstante legt damit auch fest,
wie schnell eine Adaptive Optik mindestens sein muss.
Astronomische Aufnahmen mit Belichtungszeiten kleiner als die Zeitkonstante werden als
kurzbelichtete Aufnahmen bezeichnet, d.h. die zeitlichen optischen Störungen der Atmosphäre
sind auf diesen Aufnahmen eingefroren
siehe auch Speckle Interferometrie).
In langbelichteten Aufnahmen werden die atmosphärischen Störungen
gemittelt und für Integrationszeiten sehr viel länger als die Zeitkonstante erhält man die langbelichtete PSF.
|
| |
|
Frage: Welche Werte nimmt die Zeitkonstante bei einer mittleren Windgeschwindigkeit von V=20 m/s,
einem Seeing von 1 Bogensekunde, und bei einer Wellenlänge von 0.5µm und 2.2µm an?
|
| |
|
Der isoplanatische Winkel
|
| |
|
Die langbelichtete atmosphärische PSF ist unabhängig von der Beobachtungsrichtung (isoplanar),
da die optische Turbulenz charakterisiert durch ihre Strukturfunktion statistisch an jeder
Position im Feld gleich sind.
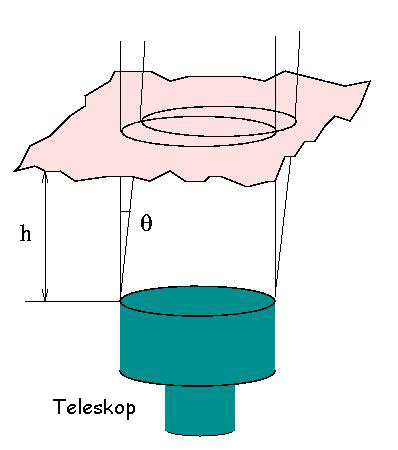
Kurzbelichtete, instantane atmosphärische Phasenstörungen hängen dagegen von der
Beobachtungsrichtung ab.
Der Teleskopstrahl (Zylinder) verschiebt sich beispielsweise
um 0.5m wenn das Teleskop 10 Bogensekunden zur Seite blickt. Die Standarddefinition des
atmosphärischen isoplanatischen Winkels ist:
\[
\theta_0 = 0.31 \frac{r_0}{H} \hspace{1cm} (14)
\]
mit einer charakteristischen, mittleren Höhe H. Dabei wird das Turbulenzprofil
\( C_n^2(h) \)
mit h5/3 gewichtet. Für typische Turbulenzprofile ergibt sich damit eine
mittlere Höhe H von ca. 5 km.
Frage:
Wie groß ist der isoplanatische Winkel bei einem Seeing von 1 Bogensekunde für Wellenlängen von 0.5µm und 2.2µm ?
|
| |
| |
| |
|
Der isoplanatische Winkel ist für die normale Adaptive Optik ein unüberwindbares Problem;
insbesondere limitiert er die Winkeldistanz zwischen Beobachtungsobjekt und Referenzstern.
Dies hat zur Folge, dass für die allermeisten Beobachtungsobjekte keine ausreichend heller
Referenzstern (Leitstern) innerhalb des isoplanatischen Winkels vorhanden ist. Diese Einschränkung führte
|
letztlich zum Konzept der künstlichen Laserleitsterne. Alternativ dazu kann eine dreidimensionale
Korrektur der Turbulenz, die so genannte Multikonjugierte Adaptive Optik (multi conjugate adaptive optics,
MCAO), das korrigierbare Beobachtungsfeld über den klassischen isoplanatischen Winkel hinaus vergrößern.
|
| |
|
Zernike-Moden
|
| |
|
In der Optik werden
Abbildungsfehler
(Aberrationen) oft als Summe spezieller Polynome, so genannter Zernike-Polynome, dargestellt.
Gleiches läßt sich für die statistischen, atmosphärischen Aberrationen machen;
jedoch sind jetzt die Koeffizienten der Zernike-Polynome die z.B. Defokus, Koma,
Astigmatismus usw. beschreiben nun ebenfalls statistische Funktionen, die sich mit der Zeit ändern.
Zernike-Polynome \( Z_n^m(r,\Theta) \)
sind in Polarkoordinaten \( (r,\Theta) \)
auf einem Einheitskreis definiert (r<1). Sie sind charakterisiert durch eine radiale (n)
und azimuthale (m) Ordnung. Für ein bestimmtes n, nimmt m
Werte von 0 bis n an. Oft wird auch statt der beiden Indizes n und m
ein einziger Index j benutzt. Für eine feste radiale Ordnung n gibt es j=(n+1)(n+2)/2
Zernike-Polynome, dabei läuft j von 1 an.
Die ersten Zernike-Funktionen bzw. Zernike-Moden haben Eigennamen wie Piston, Tilt,
Astigmatismus, Koma, Sphärische Aberration, Defokus (siehe Tabelle der ersten 15 Zernike-Polynome mit Abbildungen
und Formeln).
Ein großer Vorteil der Zernike-Polynome ist ihre
Orthogonalität.
Dies bedeutet dass das Skalarprodukt (Zi,Zj) = 1 ist
für i=j und 0 für alle anderen Fälle. Das Skalarprodukt ist definiert über das
Integral über die gesamte Teleskopapertur:
\[
(Z_i,Z_j) =
\frac{1}{\pi} \int_{|\vec{r}|\lt 1} \mathrm{d}\vec{r} Z_i(\vec{r}) Z_j(\vec{r}) \hspace{1cm} (15)
\]
Damit läßt sich nun jede Phasenaberration \( \phi(\vec{r}) \)
in der Teleskoppupille als Summe von Zernike-Polynomen darstellen:
|
\[
\phi(\vec{r}) =
\sum\limits_{j=1}^\infty a_j Z_j(\vec{r}) \hspace{1cm} (16)
\]
Die Zernike-Koeffizienten aj erhält man über das Skalarprodukt:
\[
a_j = (\phi, Z_j) \hspace{1cm} (17)
\]
In der Regel reichen bereits wenige Zernike-Moden aus, um eine ausreichend gute Repräsentation
der atmosphärischen Aberrationen zu erhalten. Korrigiert man diese, z.B. einige 10 bis einige 100
Moden mit Hilfe der Adaptiven Optik, erhält man nahezu beugungsbegrenzte Abbildungen. Der erste
Zernike-Mode, Piston, entspricht einer konstanten Phase, welche die Bildqualität nicht beeinflusst;
daher wird dieser Mode in der Adaptiven Optik zumeist ignoriert. Er spielt allerdings eine zentrale
Rolle in der Interferometrie - auch mit Adaptiver Optik.
Frage:
Ein 4-m Teleskop mit einem
Öffnungsverhältnis
von f/15, ist um 1 mm defokussiert. Wie groß ist der Zernike-Koeffizient a4 für Wellenlängen
von 0.5 und 2.2 Mikrometer ?
Frage:
Angenommen die atmosphärischen Aberrationen bestehen ausschliesslich aus Tip und Tilt mit
jeweils gleicher Stärke \( \langle a_2 \rangle = \langle a_3 \rangle = A^2 \).
Wie sieht die entsprechende Phasenstrukturfunktion aus?
Die Orthogonalität und auch Orthonormalität
der Zernike-Moden erlaubt es die Phasenvarianz über die Pupille zu berechnen. Für einen Mode ist die
Phasenvarianz \( a_j^2 \).
Die Varianz aller Moden berechnet sich aus der Summe aller quadrierten Koeffizienten beginnend mit j=2, also ohne Piston.
|
| |
|
Statistik atmosphärischer Zernike Moden
|
| |
|
Die statistischen Eigenschaften der Zernike-Koeffizienten aj
wurden von Robert J. Noll 1976 für Kolmogorov-Turbulenz berechnet. Normiert man
die Kovarianzen
<aiaj>
mit dem Faktor (D/r0)5/3
\[
\langle a_ia_j \rangle = c_{ij} \left( \frac{D}{r_0} \right) ^{5/3} \hspace{1cm} (18)
\]
erhält man nach Wang und Markey (1978), die einen kleinen Fehler in der Berechnung von Noll korrigierten,
folgende Kovarianz-Matrix für die Koeffizienten cij der ersten 11 Zernike-Moden ohne Piston (i,j=1):
|
| |